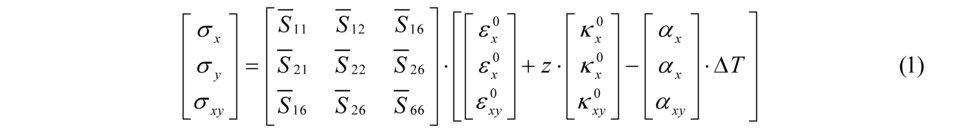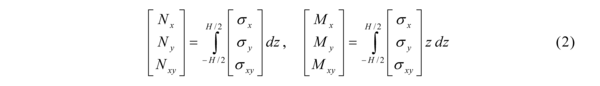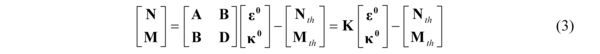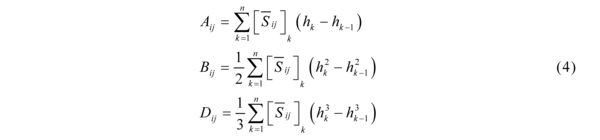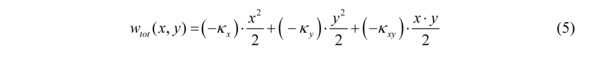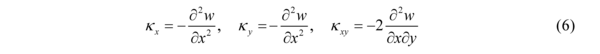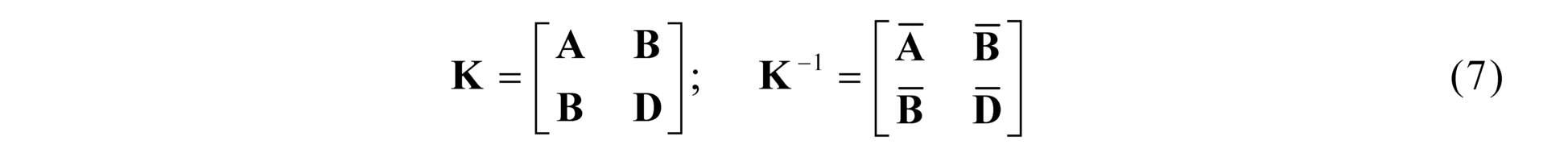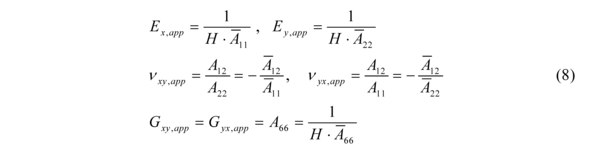Classical Laminate Theory (CLT)

Description

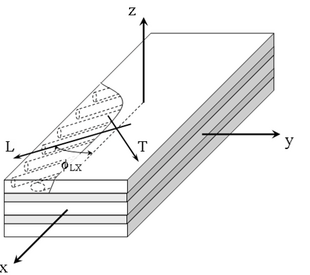
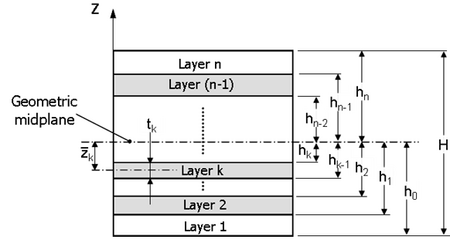
Laminate theory enables analytical stress-strain analysis of the arbitrary laminated structures (with plane laminae) subjected to mechanical or thermal load. Arbitrary number of layers, layer thicknesses and material type (isotropic, anisotropic) can be taken into account. The classical laminate theory enables to calculate stresses and strains within layers, apparent laminate properties or total deformation of the laminate (bending, twisting). Laminate theory considers always structure of the infinite dimensions, so the stresses and strains which are obtained, corresponds to the state enough far from the free edges of the real finite laminate.

 

webm-white-small_05

  (Java required)

Terms of Use

This tool is provided by ISFK to show the functionality of the classical laminate theory on the simple example of periodic laminate. The use of the tool is free of charge.

If you use data generated with the applet for your work, please cite:

Basic principle of the CLT

  • Set up the layer stiffness matrices for all layers (in XY CS).
  • Set up the global laminate stiffness matrix („Hooke’s law“ of the laminate) – using condition of the stress and moment equilibrium over the laminate height -Eqs. (1) and (2).
  • Solve the global laminate behaviour under given boundary conditions (apparent behaviour of the laminate middle plane) – Eqs. (3)-(8)
  • Calculation of the arbitrary quantities in individual layers from the global laminate behaviour substitution of results from Eq.(3) to (1).
Laminate1_01
Figure 1. Coordinate systems considered within laminate

Hooke’s law of the single layer:

EQ1

where Sij prime are components of the material stiffness matrix (transformated from LT coordinate system to XY coordinate system – see Fig. 1.),  ? - strain vector, ? – curvature vector, ? – vector of the CTEs.

Stress and moment equilibrium over the laminate height:

EQ2

By substitution of the Eqs.(1) for all layers to Eq. (2), the global laminate stiffness matrix K is obtained (the so-called A-B-D matrix – see Eq. (3)).

EQ3
EQ4

Where N, M are vectors of the boundary conditions - forces and moments. By solving Eq. (3) elongations and curvatures vectors ?0 and ?0 are obtained. By substitution of these results into the Hooke´s law of the particular layer (2), stresses at arbitrary point over the laminate height can be computed.

Laminate2
Figure 2. Scheme of the laminate uses notation

 

From curvatures ?, the total deformation of the laminate (middle plane) can be obtained:

EQ5
EQ6

To substitute all layers of the laminate by only one (orthotropic) material, the apparent material properties of the whole laminate can be calculated as follows:

EQ7
EQ8

Literature