Projects in this field:
• Ball-on-three-balls test
• Notched ball test
• Toughness measurement of ceramic materials
• Miniaturization of strength testing
• Determination of the characteristics of thermistors and varistors
• Mechanical and electrical characterization of piezo stacks
• Silicon nitride for ball bearing balls
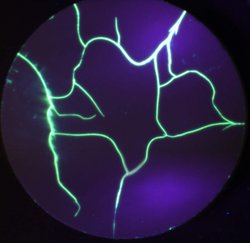
Layered ceramics have been proposed as an alternative choice for the design of structural ceramics with improved fracture toughness and mechanical reliability. The use of energy release mechanisms such as crack branching, crack deflection and/or crack bifurcation can improve the crack growth resistance of the material (Fig. 1). The use of tailored residual compressive stresses, either at the surface or in the internal layers, may also improve the strength as well as the crack resistance of the material during crack growth. In this regard, layered architectures designed with high compressive stresses can show higher strength and enhanced mechanical reliability, yielding in some particular cases a minimum mechanical resistance (threshold strength), below which the material does not fail.
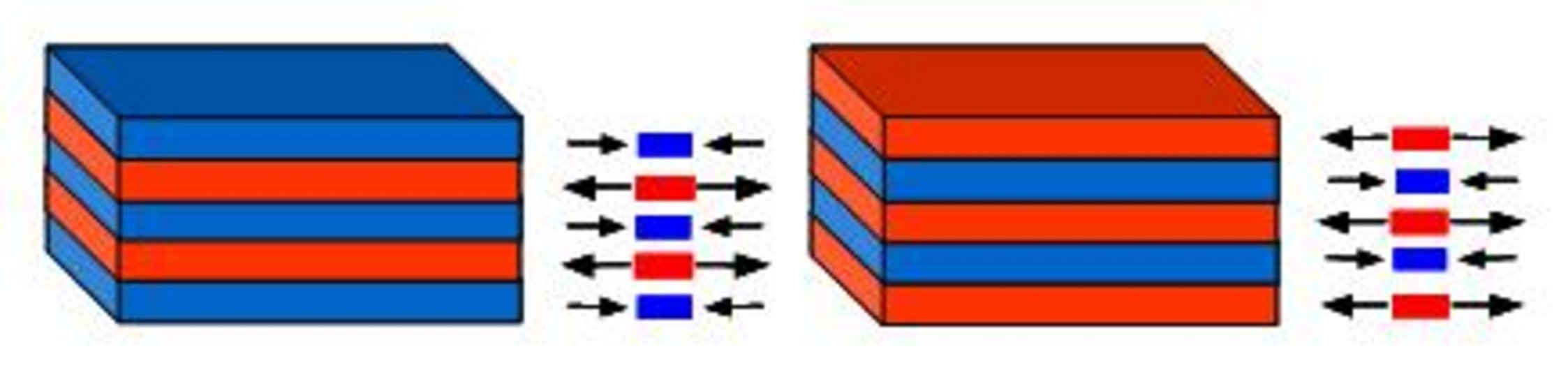
In this project design parameters to optimize the strength and toughness of layered ceramics are sought, based on Fracture Mechanics analyses and experiments. Two multilayer ceramics based on the alumina-zirconia system, designed withexternal (ECS-laminates) and internal (ICS-laminates) compressive stresses (Fig. 2), have been investigated. An optimal architecture that maximizes material toughness and strength has been found for each design as a function of geometry and material properties.
From a flaw tolerant viewpoint, ECS-laminates are suitable for ceramic components with small cracks or flaws which are embedded in or near the potential tensile surface of the piece. On the other hand, the existence of large cracks or defects suggests the use of ICS-laminates to attain a more reliable response. This analysis can be extended to other laminates which hold such energy release mechanisms.
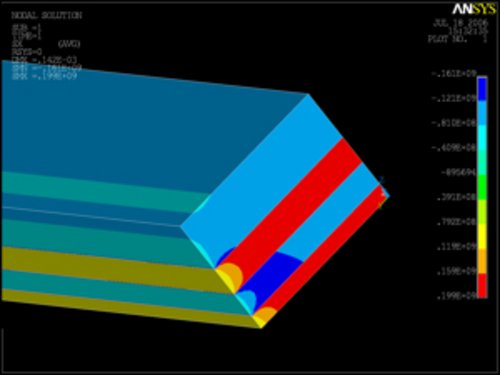
A minimum strength has been found for ICS-Laminates (threshold strength), leading to crack arrest in the compressive layers (see Fig. 3). This behaviour can be explained using a Weight Function analysis, showing that the residual compressive stresses are responsible for the toughening of the material, where the compressive layers can act as a barrier to crack propagation.
Fractography
In principle, fractographic examinations are used to analyze unexpected failures in operation, to improve a material or to examine the quality of a product.
Brittle materials fail due to the presence of defects in the material (i.e. volume defects such as pores, inclusions, agglomerates, etc.) or surface defects.
Surface defects are mainly defects that originate from surface processing (i.e. grinding) or are introduced into the surface through improper handling of the components and samples. In order to identify such defects, fractographic examinations are usually carried out after strength tests.
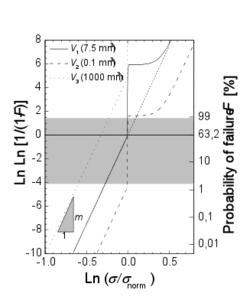
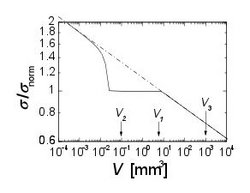
Ceramics contain a large number of small manufacturing-related "defects". They can be considered as material inhomogeneities that lead to local stress concentrations. These “defects” can be described as cracks. The failure of ceramics is usually based on such a defect (the one that causes the failure). Large defects cause low strength values. The Griffith / Irwin failure criterion predicts that the strength scales with the reciprocal of the square root of the defect size. Since the largest (fracture-inducing) defects are of different sizes in geometrically identical specimens, the strength of the specimens is also different: the strength has a large inherent scatter which can be described with a distribution function.
The topic of fracture statistics of ceramic materials has been a central research area since the institute was founded. The activities are based on the work of Danzer and Danzer et al., In which the fundamental relationship between the distribution of defect sizes in the material and the fracture statistics of samples are described. Also, the first applications of this knowledge on materials with property gradients are presented.
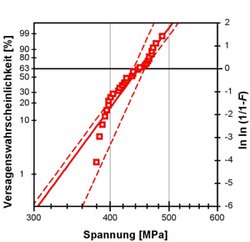
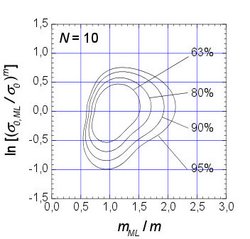
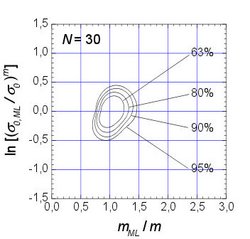
When working on fracture statistics, a large number of specimens are usually tested under defined conditions in order to obtain a distribution function for the fracture probability as a function of the fracture stress. Well-ensured experimental results that can be used as a basis for fractional statistical theories are practically impossible to obtain because of the high costs for preparing samples. Therefore, strength distributions are generated virtually using Monte Carlo simulations. In this way, typical measured values can be “generated” on the assumption that the “correct” distribution is known. Comparisons between simulated and measured samples provide important information about the material behavior. Using this method, the confidence intervals of the Weibull parameters were determined as a function of the sample size by simulating thousands of samples.
Further work shows that it is not possible to differentiate between a 2-parameter and a 3-parameter Weibull distribution with the sample sizes customary in practice (around 30 strength tests). It is also not possible to clearly determine whether a Weibull distribution, a normal distribution or a log-normal distribution is present. To do this, the sample size would have to be increased significantly.